Área de figuras planas
Area de un triangulo.
- El área de un triángulo es igual al semiproducto entre la longitud de una base y la altura relativa a esta:3
- donde b es la base del triángulo y h es la altura correspondiente a la base. (se puede considerar cualquier lado como base)
- Si el triángulo es rectángulo, la altura coincide con uno de los catetos, con lo cual el área es igual al semiproducto de los catetos:

- donde a y b son los catetos.
- Si se conoce la longitud de sus lados, se puede aplica la fórmula de Herón.
- donde a, b, c son los valores de las longitudes de sus lados, s = ½ (a + b + c) es el semiperimetro del triángulo.
- Si el triángulo es equilátero, el área es igual a un cuarto del cuadrado de un lado por la raíz cuadrada de 3:
- donde a es un lado del triángulo.
[editar]Área de un cuadrilátero
- El área del trapezoide o de cualquier cuadrilátero es igual al semiproducto de sus diagonales por el seno del angulo que forman.
- El área también se puede obtener mediante triangulación:
- Siendo:
 el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
. el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
.
- El rectángulo es un paralelogramo cuyos ángulos son todos de 90º, y el área es igual al producto de dos de sus lados contiguos a y b:3
- El rombo es un paralelogramo, cuyos 4 lados son iguales, y tiene su área dada por el semiproducto de sus dos diagonales:
- El cuadrado es el polígono regular de cuatro lados; es a la vez un rectángulo y un rombo, por lo que su área puede ser calculada de la misma manera que la de estos dos. En particular, dado que sus lados son iguales, se usa la fórmula:3
- El trapecio, el cual tiene dos lados opuestos paralelos entre sí y dos lados no paralelos, tiene un área que viene dada por la media aritmética de sus lados paralelos multiplicado por la distancia entre ellos (altura):3
[editar]Área del círculo y la elipse
El área de un círculo, o la delimitada por una circunferencia, se calcula mediante la siguiente expresión matemática:4
El área delimitada por una elipse es similar y se obtiene como producto del semieje mayor por el semieje menor multiplicados por π:5
[editar]Área delimitada entre dos funciones
Una forma para hallar el área delimitada entre dos funciones, es utilizando el cálculo integral:
El resultado de esta integral es el área comprendida entre las curvas:  y
y ![g(x) [< f(x)]\,](http://upload.wikimedia.org/math/1/d/3/1d3507ab25c5f1c6f1f965b2397293c3.png) en el intervalo
en el intervalo ![[a,b]\,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) .
.
 y
y ![g(x) [< f(x)]\,](http://upload.wikimedia.org/math/1/d/3/1d3507ab25c5f1c6f1f965b2397293c3.png) en el intervalo
en el intervalo ![[a,b]\,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) .
.- Ejemplo
Si se quiere hallar el área delimitada entre el eje x y la función f(x) = 4 − x2 en el intervalo [ − 2;2], se utiliza la ecuación anterior, en este caso: g(x) = 0entonces evaluando la integral, se obtiene:
Por lo que se concluye que el área delimitada es 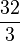 .
.
El volumen encerrado entre dos funciones también puede ser reducido al cálculo de una integral, similar.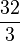 .
.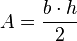
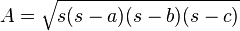
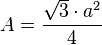










![A(-2,2) = \int^2_{-2} | 4 - x^2 - 0 | dx = 2 \int^2_0 4 - x^2 dx = 2 \left[ 8 - \left(\frac{2^3 - 0}{3}\right) \right] = \frac{32}{3}](http://upload.wikimedia.org/math/0/6/7/06719bebf0dff05ea21b3370585d4927.png)
No hay comentarios:
Publicar un comentario